Explainer: Supply Constraints do not Explain House Price and Quantity Growth
A detailed look at a recent working paper that is making waves amongst housing economists
An article like this would usually be for paid FET subscribers only. But in the interest of enhancing the quality of our economic and policy debates, it is free for all. Please consider financially supporting Fresh Economic Thinking if you can.
A recent working paper by Schuyler Louie, John A. Mondragon, and Johannes Wieland has been making waves in urban economics circles. The paper title might provide a clue as to why— “Supply Constraints do not Explain House Price and Quantity Growth Across U.S. Cities”.
The effect of land-use regulations on housing affordability is a polarising topic. Unsurprisingly, everyone seemed to interpret this paper in line with their prior views.
Those who think removing planning regulations won’t automatically bring down the asset price of homes through faster home building had their view supported. Those who think the opposite went looking for methodological errors, figuring the results couldn’t hold without it.
More on that later.
The plan for this article is to step through this paper so as to explain in an accessible way how the authors (whom we abbreviate to LMW) went about their analysis. What did they find, and how did they find it? We have clarified many of the finer details with the authors, and we hope our summary is fair and useful.
As background, one of us undertook a similar study in a 2022 paper with Mark Limb, which compared long-term changes in prices and quantities between upzoned and non-upzoned areas. You can download that paper below.
What is the question?
Some of the controversy around this paper may be due to readers misunderstanding the question. One paper can’t tell us everything about housing markets.
This paper does one important thing. With the data at hand, it asks a simple yet fundamentally important question:
Can we observe differences in how the price and quantity of homes changed between 1980-2020 across what are claimed to be less and more supply-constrained cities that experienced similar changes in housing demand over that period?
It’s commonly claimed that regulation and land availability limit how fast housing supply can respond to growing demand, leading to faster-rising prices and fewer new homes in more constrained cities. A number of studies measure these so-called “supply constraints”, claiming they are a cause of price differences between cities.1
But if we can’t see this difference in the data, then maybe what is being measured by the supply constraint metrics that LMW examine is not an economically meaningful cause of prices. Maybe we need to think differently about the causes of housing prices and production, and maybe the idea of an independent supply curve for housing is not the right way to understand housing markets.
LMW did not find the expected pattern in the data. That explains the title of their paper, and their conclusion that “housing supply constraints are quantitatively unimportant in explaining rising housing costs across U.S. cities”.
What is the expected answer?
When we start with a certain theory about the economic determinants of home prices and quantities, we expect to see a certain pattern in the data.
The theory tested here is that for each city there is a thing called a housing supply curve which exists independently of demand, has a slope determined by physical and regulatory constraints, and determines how many houses will be produced at any given price level.
The theory also assumes the existence of an independent demand curve, which tells us how many homes will be bought (or consumed) at each price level. Since the production and consumption of homes must be equal, there must exist a market equilibrium in which this supply and demand jointly determine the housing asset price and quantity.
At its most basic, the assumption here is that the market for houses can be studied as if it has independent supply and demand sides—that what buyers are prepared to pay for housing assets is independent of what sellers are willing to receive to part with them. This is a standard ECON101 approach to explaining market outcomes, so it’s natural to think it can be usefully applied to housing.
This standard theory also predicts how markets respond to change. When the number of buyers and the price they are willing to pay increases—when demand rises—the change in price and quantity will depend on the elasticity of supply (the slope of the supply curve). This elasticity is commonly thought to be determined largely by planning regulations and geography—the so-called supply constraints. Policy to relieve these is therefore thought to reduce prices via more elastic responses to demand growth.
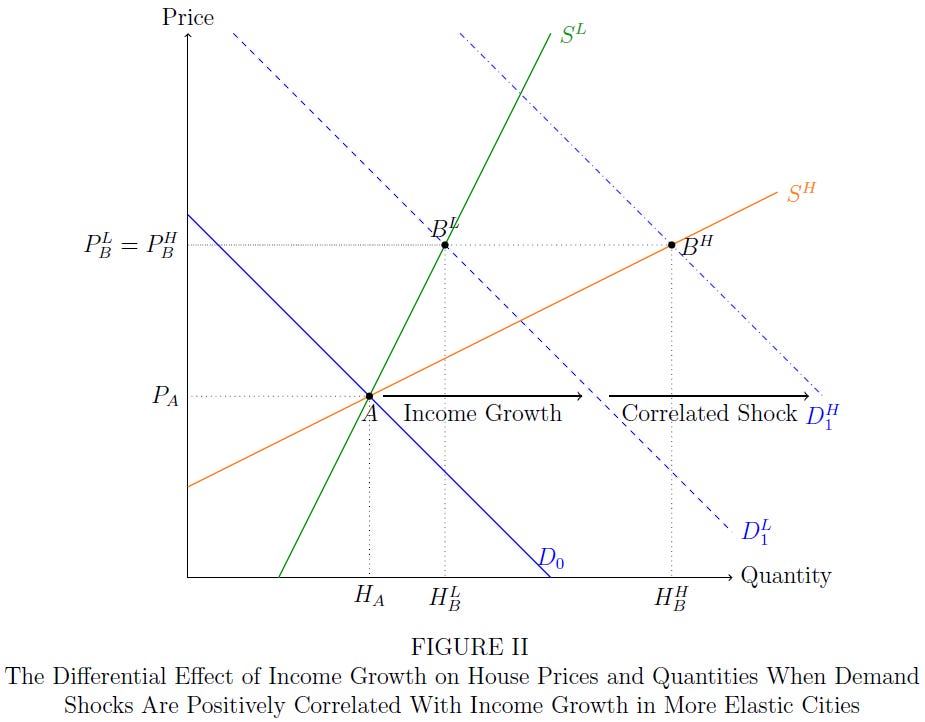
The diagram above from LMW’s paper shows the theory their analysis tests in relation to supply elasticities across U.S. cities. It shows the expected pattern in the data if these supply constraints—measures of the physical and regulatory environment made in prior studies—are truly a good proxy for the slope of the supply curve in each city.
If this were true, more constrained supply conditions would show up as a steeper (less elastic) supply curve, like the green line, while less constrained supply would show up as a flatter (more elastic) supply curve, like the orange line.
For any given change in demand (the blue line) we should see a difference between less constrained and more constrained cities in how prices and quantities change over time.
To test whether measured supply constraints truly affect the supply elasticity and growth in prices over time we need to test whether, at any given rate of demand growth, house price growth is higher and quantity growth of the housing stock is lower in cities deemed to have more constrained supply.
Side note: Cameron has long argued that thinking about housing production being economically determined by a static supply curve that is input-cost-based and independent of demand is misconceived. Since the economic cost of producing a new home is the return from waiting until a future period to develop the land, we should instead think about housing production as a flow that takes place at an equilibrium rate (an absorption rate) determined by asset returns, specifically the returns to undeveloped land. Thinking about housing production based on input costs, including those arising from regulations, taxes, or geography, will mislead us. More details on this approach are in this FET article.
How the answer was determined
For each of the 300 or so U.S. cities in their sample, LMW first gather metrics thought to represent the extent of supply constraints caused by physical (geographic) and regulatory factors. These constraints are commonly believed to determine the responsiveness of supply to price (the slope of the supply curve).
LMW use four different supply constraint metrics:
A supply elasticity estimate from Saiz (2010), inferred from measures of regulatory and geographic supply constraints.
A second supply elasticity estimate from Baum-Snow and Han (2024), likewise generated from a predictive model based on supply constraints.
The Wharton Residential Land Use Regulation Index (WRLURI) from Gyourko, Saiz and Summers (2008), in which more regulation is considered to reduce elasticity.
The land share of house value from Davis, Larson, Oliner and Shui (2021), which is meant to reflect the idea that supply constraints show up in higher land value shares.
The Wharton index is inverted, and the Davis et al land value share is converted to a building share (one minus the land share) in order that higher numbers for all four of these metrics represent what are presumed to be less constrained supply conditions.
LMW also collect census data on the stock of homes in each city (each metropolitan statistical area, or MSA) and total income, using county-level personal income aggregated to MSA areas. Two different data sources are used for the asset price of homes: the Corelogic single-family repeat sales index and the American Community Survey (ACS) measure of median home value. All the data runs from 1980 to 2020.
Together, there are four main data points for each city: growth in the housing stock, growth in the housing price, growth in total income, and a supply constraint metric.
What does the data look like?
The first result is that these supply constraint metrics correlate with house price growth, confirming what has been established by others.
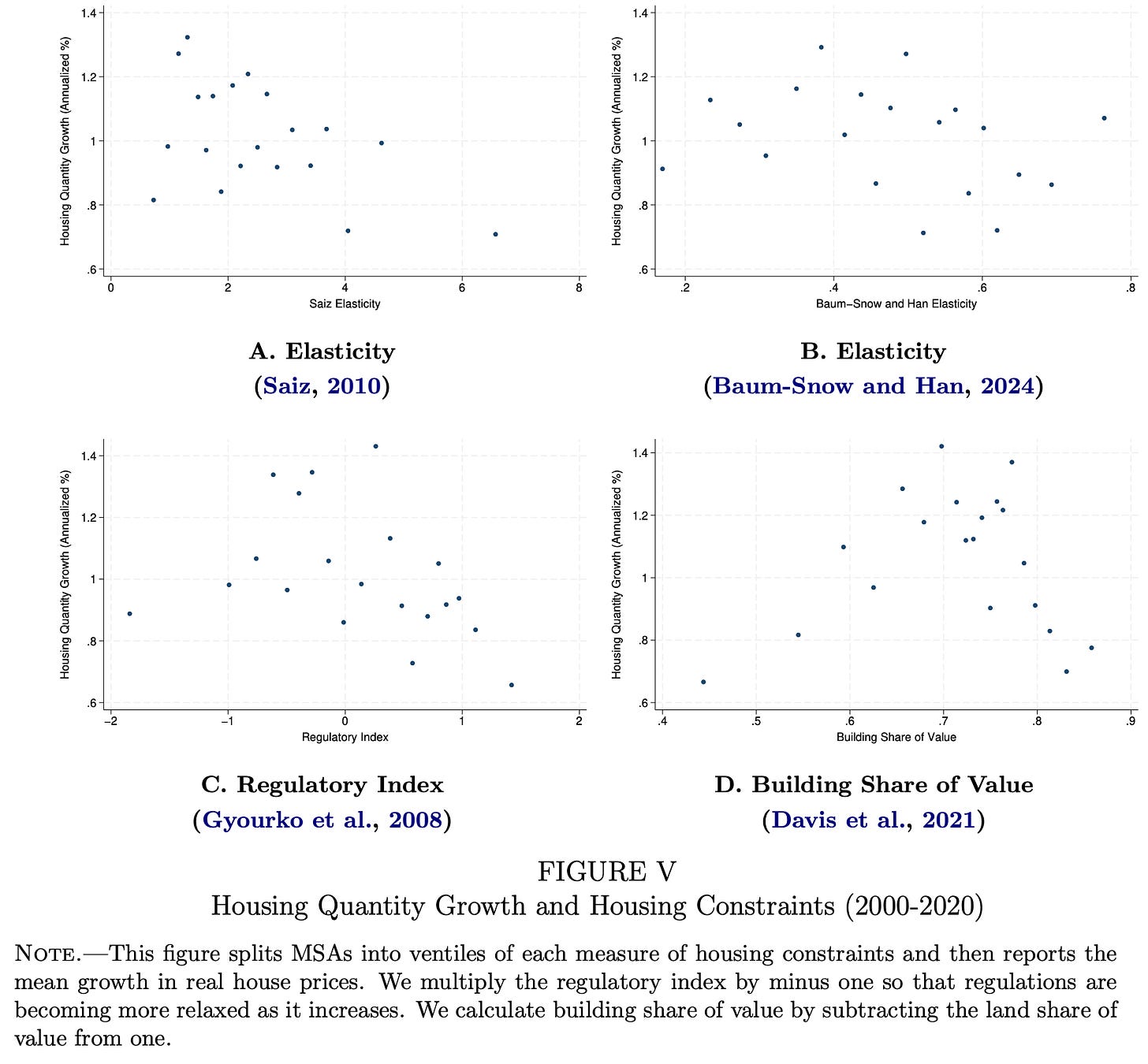
Figure IV from the paper, shown below, plots the relationship between each of the four supply constraint metrics (on the X-axis of each chart, with higher values representing less constrained supply) and real inflation-adjusted annualised house price growth (on the Y-axis of each chart). The data is for the second half of the 40-year study period, i.e. 2000-2020.
Each point in the chart is the average of a 5% segment of the data (a ventile) when ordered by the supply constraint metric (meaning there are 20 points in each chart instead of 300, as would be the case if every single city was plotted).
The negative correlation is clear to see: less constrained cities had systematically lower house price growth between 2000 and 2020. This is just what we’d expect if these supply constraints were affecting supply elasticities.
Case closed, right?
Not quite.
If supply constraints were determining supply elasticities, then lower price growth in less constrained cities would have resulted from more new homes being built. We should therefore see that extra construction in the data. As LMW note, “housing quantities should reflect the inverse relationship” (to the price relationship in Figure IV).
But they don’t. The data doesn’t support that story.
Figure V from the paper is shown below. It has the same setup as Figure IV above, but with housing quantity growth instead of price growth on the Y-axis.
There is no upward slope. But if lower house price growth in less constrained cities had been caused by higher housing production, not by some other factor unrelated to supply, there would have been.
The data is showing us “missing homes” in less constrained places compared with what we’d expect if lower price growth in these places had been caused by higher elasticities of supply.
This pattern of missing homes flows through to all the results in the paper.
What can explain it?
One answer is that the combination of lower price growth and missing homes in less constrained markets perhaps reflected that people didn’t want to move there—that there was no demand for housing, so none was built.
This is where total income enters the analysis.
The authors test whether housing markets in less and more constrained cities responded differently to the same increase in total income (population times average income).
If no one had moved to less constrained cities, then fewer new homes would have been built, regardless of the shape of the supply curve. Nor would many new homes have been built had incomes not risen, and had people been unwilling to pay for more or bigger homes. So to test whether less constrained cities had systematically higher supply elasticity, as is often claimed, LMW need to measure price and quantity changes after controlling for the change in demand.
Can slower growth in demand explain the lower price growth and missing housing in the less constrained cities?
LMW use total income (which captures changes in both average income and population) as a proxy for demand. Had supply constraints truly affected house price growth as supposed, cities with the same change in total income but different supply constraints should have seen different growth in prices and housing quantities.
Did they?
To test this as simply as possible, LMW split their data into two. Cities with above-median supply constraint metrics were put into a more constrained group, and cities with below-median supply constraint metrics were put into a less constrained group.2 These groups should have supply curves like the green (inelastic) and orange (elastic) curves in Figure 1 above, respectively, and should therefore have exhibited different price and quantity responses to income growth.
LMW test this by measuring price and quantity growth while controlling for income growth.
First, price growth.
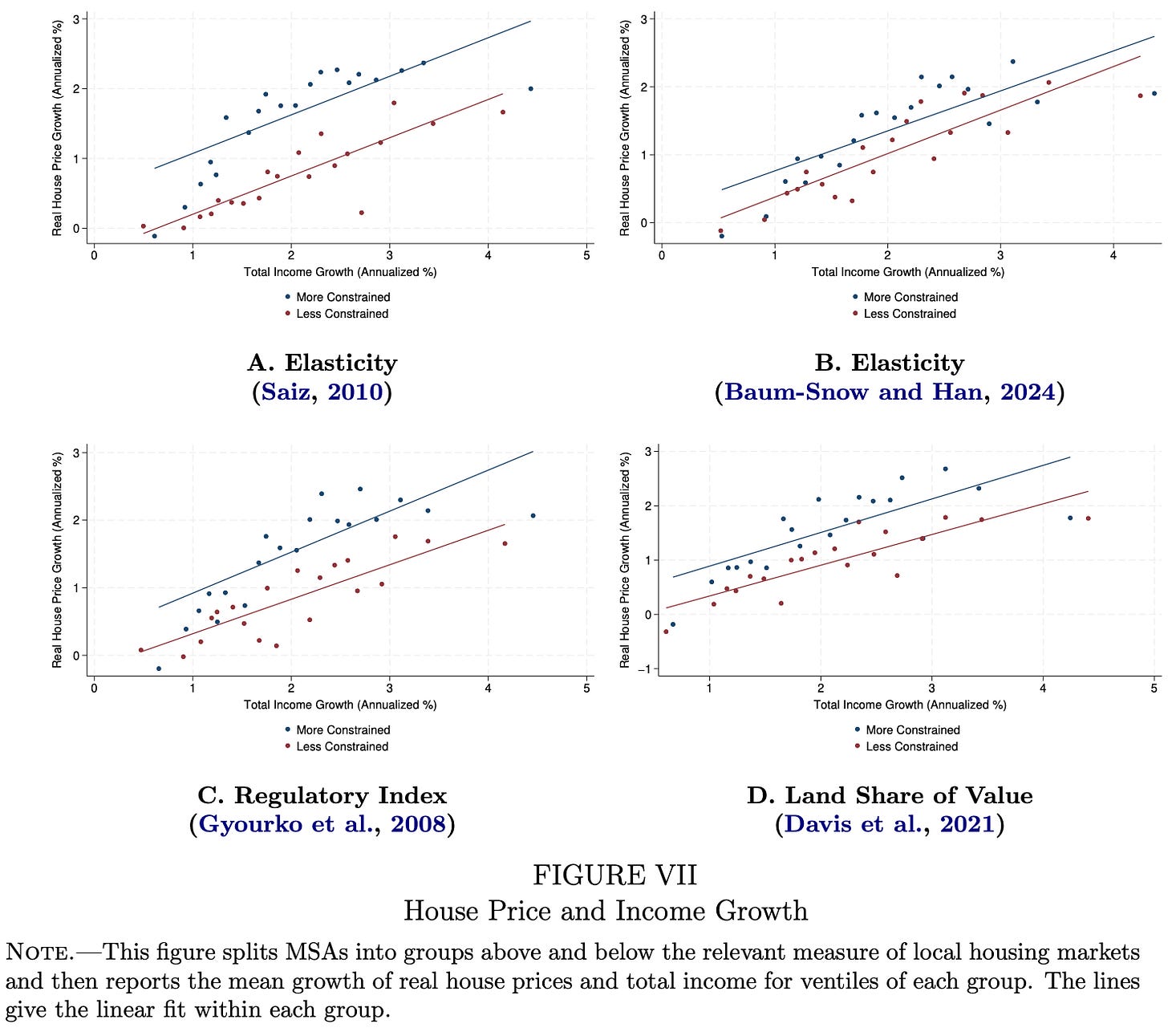
Figure VII from the paper is shown below. The more constrained group of cities is shown in blue and the less constrained group in red.
Once again, we see slower price growth in less constrained cities, across the whole range of income growth. For any given rate of income growth (any point on the X-axis), less constrained cities had lower price growth than more constrained cities (since the red line is below the blue line).
But we run into two problems when interpreting this as evidence of differing supply elasticities.
First, a fixed vertical gap between the two lines isn’t what the theory predicts. These lines should look like the orange and green supply curves in Figure 1—the red line should be flat like the orange supply curve, and the blue line should be steep like the green supply curve. If demand grows a lot, e.g. by 4% per annum instead of 2% per annum, the difference in the percentage point rate of price growth between less and more constrained cities should be higher, not the same.3 In short, less and more constrained cities do not show price growth differences consistent with a supply-elasticity explanation of how supply constraints affect prices.
This raises a new puzzle: why, if the elasticity explanation does not seem to hold, do less constrained cities still have lower price growth after controlling for demand?
Second, the pattern of missing homes in less constrained places is still there, as we see in LMW’s Figure VIII below. Had supply constraints truly explained price differences via their effect on quantity, we should have seen a relationship between supply constraints and quantity growth that is the opposite to that for price growth in Figure VII—for any given increase in total income, less constrained cities should have built more new housing.
But Figure VIII shows no difference between less and more constrained cities in housing quantity growth at any level of income (since the red and blue lines are effectively identical).
In LMW’s dataset, the construction response to rising income does not appear to depend on measured supply constraints. We cannot see the data signature of a systematic difference in supply elasticity arising due to differences in regulatory and geographical constraints.4
To explain why certain cities have lower price growth at any given level of income growth, we need some other story. We return to this later.
Testing the answer
Let’s recap:
U.S. cities with fewer regulatory and geographical constraints on home building had lower house price growth from 2000-2020 (Figure IV).
This was true regardless of demand growth, as proxied by total income growth (Figure VII).
But had this been caused by more elastic supply in these cities, it would have been accompanied by higher quantity growth (as per Figure I).
It wasn’t: at every rate of total income growth, less constrained cities built no more new housing over the period than more constrained cities (Figure VIII).
Lower price growth in these cities must have occurred for other reasons—not because fewer supply constraints caused new supply to respond more elastically to demand growth.
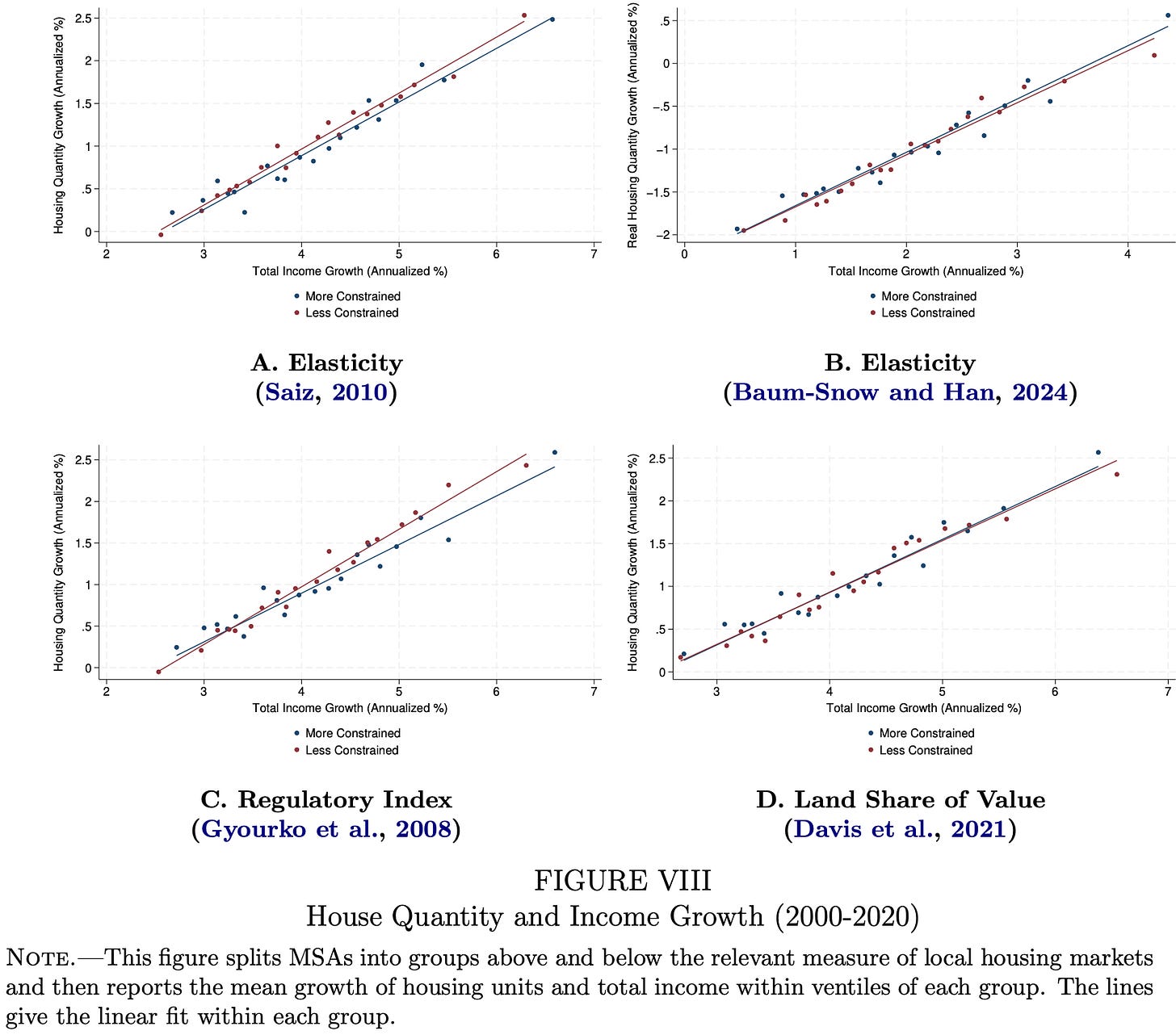
We’ve told this story in charts, but LMW also establish all of the above via regression analysis.
Is there more to the analysis? Yes. LMW try to disprove their main result with a series of robustness tests, but each extra piece of analysis essentially confirms the story in the charts above.
LMW test different measures of home prices and quantities, such as population growth and rooms per capita.
They extend the sample to 40 years (from 1980-2020) and test the subsample of 1980-2000.
They use quartiles for the supply constraint metrics instead of binary low/high groups.
They argue that the price growth levels effect in Figure VII “is quantitatively small and unlikely to reflect a causal effect from the supply elasticity on house price growth.”
And finally, they consider the idea that a 20-year or 40-year period of analysis is too long to detect the true effect of supply constraints. Maybe supply constraints affect construction over the shorter term, but macroeconomic adjustments dominate housing market outcomes over these longer periods of time?
Two of the authors, Mondragon and Wieland, have previously analysed the effect of work-from-home trends on housing markets. They argue here that the sudden increase in remote work over the pandemic functions as an unexpected demand shock suitable to test the theory that short-run supply responses to demand shocks differ between less and more constrained cities.
Using data from 2019-2023, LMW ask whether less constrained cities saw lower price growth and higher housing quantity growth than more constrained cities that experienced similar increases in remote work. For this test they use annual permits rather than growth in the housing stock (which changes only slowly).
Once again, they detect no measurable differences in the change of prices and quantities across what are presumed to be less constrained and more constrained cities that experienced the same unexpected short-run demand shock:
In short, we show that even in an episode that is out of sample and where we have isolated plausibly exogenous variation, these measures of housing constraints do not affect the relative growth of house prices and house quantities across cities. Once again we conclude that differences in housing supply elasticities are quantitatively unimportant for explaining differences in house price and house quantity growth.
Making waves
The splash made by this paper amongst urbanists and housing economists is partly due to:
The provocative title and direct, clear writing.
A popular misconception about the state of economic knowledge about why homes are built.
The former was necessary given the latter. Let us dwell for a moment on this misconception before considering the critiques levelled at this paper.
Some people imagine the science of why homes are built is settled.
This is far from true. Our work has repeatedly explained the limits to our collective understanding of housing supply and the limited utility of the static supply and demand model.
Yes, every trading equilibrium reflects supply and demand for the traded good or asset—every seller must find a buyer. But what supply/demand equilibrium really matters for house prices? Equilibrium trades of existing housing? Equilibrium construction? Equilibrium stock?
People claiming housing outcomes are simply “supply and demand” without a theory of the underlying causes of production are missing the point: those causes are far from self-evident. If you don’t yet appreciate why recourse to supply/demand begs all the important questions, consider this question-and-answer logic:
Q: What causes the housing supply curve? A: Supply costs.
Q: What are those costs? A: Land and construction.
Q: What causes land costs? A: Demand for housing.
Either the all-important question of where land costs come from remains unanswered, or the axioms of supply/demand analysis—two independent curves—are breached.
Produced goods have costs independent of demand. Land does not. It has no production cost. And the opportunity cost of developing it is foregoing the option to develop it later, the value of which depends on demand.
Because the static supply/demand model ignores time, it is incapable of reflecting the fact that the cost of supplying a home today is the benefit of waiting for tomorrow.5
People ignoring this intertemporal margin often wind up conflating the equilibrium density of new homes (dwellings per land area) with the equilibrium rate of production (dwellings per time period). As a consequence, many assume that deregulating planning to allow “more homes” (per area) is the same as getting more homes per period.
If you want to be clear on this point, read this article.
And to understand the many margins of housing market equilibrium—asset prices, rents, location, density, and the absorption rate—try this article.
So the theory of what causes homes to be built is far from settled.
But the empirical evidence that regulatory constraints affect the rate of new supply is also much weaker than most assume. Findings like LMW’s are common. Tom Davidoff in a 2016 paper, for example, found that “housing supply has grown more in supply-constrained markets than elsewhere over recent decades”.
He explains:
Economists sometimes assume that strictly regulated housing markets near mountains and oceans are expensive because they are costly places to build, not because they are nice places with productive firms and workers. U.S. data show this convenient assumption to be false.
Davidoff interprets his findings as “indicating constraints are correlated with demand growth”. That’s one interpretation. Equally, it could be that the physical and regulatory factors commonly assumed to be supply constraints are not constraints on the quantity of homes, but are only constraints on where and what type of homes are built in each city. The evidence in LMW’s paper supports the latter interpretation.
Reaction and critique
LMW’s paper prompted a swift reaction from urbanists. Some strawmanned it as assuming that supply and demand don’t apply to housing. The image below shows a few such comments, illustrating the tribal psychology at play.
The paper has also prompted two thoughtful critiques—one by Salim Furth (here) and one from Michael Weibe (here).
What are these critiques, in simple terms?
There is a simple and seemingly misguided critique, already dealt with in the paper, and a more subtle critique of econometric technique, which hits the mark but seems not to affect the results.
Total income growth includes population change
Furth and Wiebe point out that population and therefore total income (population times average income) is ‘endogenous’ to (caused by) local supply conditions. If more constrained cities build fewer homes, as people claim, then fewer people will move there and they will have lower total income growth.
Figure VIII above showed that less constrained and more constrained cities had the same quantity growth at each level of total income growth.
The critique says that an identical level of income growth across two cities might be the result of quite different underlying demand growth, if it was the case that lower demand to move to less constrained cities was fulfilled while higher demand to move to more constrained cities was not. Relative supply constraints, in other words, shift population around—tight constraints limit construction, deter population growth, and cause cities with fewer constraints to absorb more people.
Since total income isn’t independent of measured supply constraints, these critics say, it’s a poor proxy for demand: it doesn’t cleanly identify the underlying demand shocks to which we wish to measure supply responses. It identifies the total effect of underlying change in demand to live in a place interacted with how well that place accomodated growth.
This seems like a killer critique.
But the authors don’t think so. They already covered it in their paper.
Indeed, the use of total income should actually make it easier, not harder, to detect differences in underlying supply elasticity from the data, if they are truly present in reality. If population growth truly reflects supply constraints, then using total income (unlike average income) will amplify variation in price and quantity change in the dataset, making it easier to identify any statistically significant effects.
Let’s step through this.
First, LMW agree that:
since growth in total income reflects growth in population as well as growth in average income there will be a tight relationship between housing quantities and total income growth (p16)
But they also argue that no matter what drives total income growth—whether it is purely ‘exogenous’ factors (e.g. rising wages) or also endogenous responses (e.g. higher migration due to lower housing costs)—the correlations between total income growth on the one hand and quantity and price changes on the other still reveal the true elasticity of supply. This is a key point.
The statistical challenge they face is to uncover the unknown shape (slope) of supply curves across different cities. Any source of variation in demand—wage growth, population growth, rising amenity, anything at all—produces variation in price and quantity data, helping to reveal that slope. The fact that a flatter slope might correlate with faster demand growth by way of higher migration and thus higher total income growth over the 20-year study period does not itself affect the measurement of relative price and quantity changes and therefore affect how accurately the slope of the supply curve (the elasticity) is measured.
Their Figure II, below, explains this clearly.
Suppose some shock like rising wages is common across cities (the first shift in the blue demand curve). This will cause high price growth in low-elasticity cities (with green supply curves). Now suppose this spurs migration to high-elasticity cities (represented by a second shift in the blue curve, which applies only to cities with orange supply curves). It’s clear that the final price and quantity effects of this two-stage process still accurately reflect the slope of the true underlying supply curves in the two city types. Indeed, using total income—which reflects both demand shifts, not just the first—will amplify variation in the data, helping reveal any true differences in elasticity.
If regression analysis can’t detect any difference in slope, then what are claimed to be supply constraints aren’t actually constraining supply (i.e. reducing supply elasticity). If supply truly is more elastic in less constrained cities, we ought to see evidence of this in the relative price and quantity changes for those cities, no matter that those changes are the result of feedbacks between supply, demand growth, and total income via migration.
A second, more technical, critique by Wiebe is that if supply constraints truly do affect supply elasticities and thefore affect migration and total income, then grouping low- and high-constraint cities means grouping cities of differing elasticity, which renders the particular equations LMW derived to estimate group-level elasticity wrong.
The response from LMW is here and downloadable below. It acknowledges the in-principle problem with their derivation. But it also demonstrates that the bias this problem produces is small, and indeed, is more likely to over-estimate elasticity differences between cities than suppress them.
Why do more constrained cities have high prices?
Salim Furth, in his critique, asks:
And if the authors’ interpretation is correct, then the tall task remains of explaining why prices have risen so much more in the quartile of metros that previous authors have identified as constrained?
There are many candidate explanations.
First, people cluster in places by income and industry, which makes for expensive and cheap places within and between cities. In spatial equilibrium, migration equalises quality of life, and house price differentials reflect amenity and productivity differences—affordability advantages don’t last. This has always been the case, and physical limits on location make it so. Faster rising prices in certain places are part and parcel of adjustments to this equilibrium.
Second, the supply constraint metrics themselves reflect feedbacks from prices to constraints that can cause a correlation between more constraints and higher prices. Residents of wealthier areas place a premium on protecting their amenity and de-risking asset ownership, and choose more specific and robust regulations to achieve that. Such reverse causality prevents simple inference about how regulation affects prices, as Cameron explained in a paper with Peter Phibbs, discussed here.
Third, and in the other direction, supply constraints could affect amenity. Looser regulations may reduce amenity via negative externalities, while also increasing the perceived risk that nearby development will reduce the value of specific housing assets or alter the neighbourhood character most valued by current residents. Negative externalities and higher risk both reduce prices.
None of these explanations trace causation from constraints to prices via quantities—the supply-side story. They simply involve location-specific amenities and prices correlating with constraints. Higher-priced locations choose tighter constraints than low-priced locations, and those constraints then affect amenity and price directly via demand, not via supply responses.
Fourth, and finally, an issue not raised in either critique is the use of housing asset prices as a measure of the price of housing. House asset prices vary relative to the rents they earn due to changing yields in asset markets and property taxes (which reduce prices).
Different property tax rates between less constrained and more constrained cities could explain the outstanding puzzle of the level differences in price growth over the study period.
Let us explain.
When house prices rise to keep housing yields in line with falling asset yields across the economy, as they did over LMW’s four-decade study period, houses in high-property tax jurisdictions will exhibit mechanically lower price growth, by way of those higher taxes demanding higher pre-tax (or ‘market’) yields. Think here of cities in Texas, and specifically Houston, where property taxes can be roughly 2% of the property value each year. Those yields fall by proportionately less in an environment of falling economy-wide yields than they do in low-tax jurisdictions, where market yields are lower.
The table below demonstrates this. To preclude arbitrage, after-tax yields (not market yields) must equalise across locations. In high property tax locations, this requires higher market yields (equivalently, lower asset prices). When economy-wide yields and after-tax housing yields fall, in this example from 5% to 3%, the asset price, which capitalises net rent according to the market yield, rises by proportionately less in high-tax locations than in low-tax locations.
Some cities are also seen as less risky places to invest in housing. Amid declining overall yields, lower-risk locations will see higher price growth than more risky locations due to higher relative yield declines.
The correlation between measured supply constraints and property taxes is worth exploring as an explanation for differential price growth. For at least one supply constraint metric, the building share of value, the correlation should be clear: property taxes are capitalised into lower land values, not building values, so the building share of value will be higher when taxes are higher, regardless of regulatory or geographical constraints.
So what?
LMW’s paper is a high-quality attempt to answer one simple yet fundamental question about the causes of housing prices, and has become a topic of much debate amongst urbanists, planners, and housing economists for that reason.
This ‘explainer’ is our attempt to help this conversation along. With many people finding LMW’s results counterintuitive, and with several critiques now in circulation, we saw value in explaining the method clearly.
Rather than being an outlier, LMW’s results add to a range of research that contradicts the claim that geographic and regulatory constraints reduce the elasticity of new housing supply and force house prices higher.
That the rate of price growth in LMW’s paper correlates closely with the rate of quantity growth is more consistent with an absorption rate theory of equilibrium housing production than a theory about regulation and elasticity.
LMW’s finding that for any given rate of income growth housing asset price growth is lower in less constrained cities still requires an explanation, however.
We’ve suggested a range of reasons, which relate to spatial equilibrium and reverse causality in the construction of supply constraint metrics. Our own novel suggestion in this regard is that asset pricing factors, specifically differentials in property taxes and city-specific risk (and therefore pre-tax housing yields) are capable of explaining some of this pattern in the data.
Further analysis on how asset pricing factors, spatial equilibrium forces, and equilibrium rates of new housing production relate to asset prices would be welcome.
If you have come this far, I recommend this article explaining a better way to understand how housing rent, prices and production are determined.
As always, please like, share, comment, and subscribe. Thanks for your support. You can find Fresh Economic Thinking on YouTube, Spotify, and Apple Podcasts.
Interested in learning more? Fresh Economic Thinking runs in-person and online workshops to help your organisation dig into the economic issues you face and learn powerful insights.
Throughout this piece we’ve italicised the words supply constraints, less constrained and more constrained, which is the language used throughout LMW’s paper. Our purpose in doing this is to emphasise that the idea that geographic and regulatory factors constrain the rate of supply of new housing in ways that affect house prices is a claim that remains in contention, and indeed is the very claim being tested in LMW’s paper.
Splitting the data like this into two bundles is a simple way to detect a difference between less and more constrained cities. Later, the authors also split cities into quartiles. We expect the authors will extend this to regressions where the supply constraint metric is a continuous variable, and we suspect, given the patterns in the data, this will confirm the basic story evident from the binary and quartile splits.
This point isn’t actually self-evident from Figure I, which simplifies the exposition by showing linear supply curves. However the logic holds in the model equations used by LMW, which have more realistic functional forms (it can be inferred from LMW’s equation 1).
To make this point explicitly, LMW also estimate a supply elasticity for each city by way of an instrumental variables regression approach, which first isolates the price effect of rising demand, then estimates the quantity response to this price effect. The estimated elasticities are no different across less and more constrained cities.
It has long been known that in asset markets, delay is the cost of building. Way back in 1939, Harold Hotelling explained the equilibrium rate of coal production from known reserves as an equilibrium between the benefit of waiting (cost of extracting) and the benefit of extracting (cost of waiting), which I discuss in this article.












Thanks for this great explainer. This fits well with your emphasis on the need for better economic theory to understand housing markets and your critical work, such as "Evidence-Lite Zone". There are theoretical simplifications that are linked to statistical work that attributes too much causation to correlations, despite 'controlling' for this and that. All of this aligns with my own view that far too much weight has been placed on regulation as an exogenous barrier and not attention on the endogenous layering of forces that are housing markets. If I can add a simple example, if the clustering by income and the positive amenity affects of valuable locations and densification create higher land values, that may induce land owners to expect escalationg prices and to reduce their willingness to sell in the present but wait for even higher prices. There are feedback effects here. If something like this is happening, then as D shifts out due to higher incomes and higher amenity (just what Glaeser used to argue in his "Consumer City" pieces) then higher land prices are an increased cost on the S side. In short, a Demand increase will cause the S curve to also shift upward or to steepen (lowering elasticity) and this will further increase housing prices. No regulation needed to grasp this effect, just an endogenous link between increased willingness to pay and the price needed to induce more supply. I think areas with higher housing prices, such as coastal California and parts of the US eastern seaboard, have been leaders in this process and that the dynamics of a longer-term increased willingness to pay to live in valuable urban spaces is unfolding across the US and in other places too. This is a historical shift related to incomes, lifestyles, and the complex dynamics that sets off in the housing markets. Regulation that protects higher income areas from rental housing and lower-income residents is pernicious in itself as I see it. This requires targeted opposition on equity grounds, but this is not the same as the broader faith in de-regulatino as the 'solution' to an inadequately understood housing crisis. Thanks for your continuing to link policy to more nuanced theory! This is desperately needed before we over incentive developement in ways that we may regret as a new type of 'urban renewal'
This theory seems like it requires developers to be able to costlessly hold onto land indefinitely, which isn't realistic for most developers who use leveraged financing and face interest payments, face carrying costs like property taxes/ongoing site security, and would encounter capital constraints when they go to their next deal.